MÚSICA Y MATEMÁTICAS. LA ESCALA DIATÓNICA
P
ero… ¿Dónde comenzó todo? ¿En dónde situamos los orígenes de la música occidental? Para responder a estas preguntas tendremos que hacer un largo viaje en el tiempo hasta la Antigua Grecia y conocer de cerca la escuela que fundó Pitágoras de Samos a mediados del siglo VI a. de C.
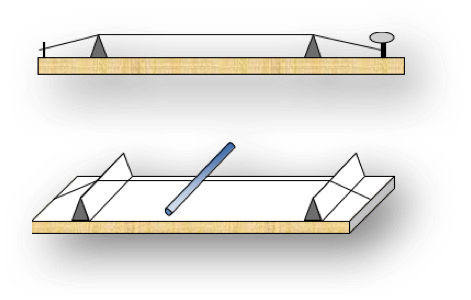
Pitágoras descubrió una conexión entre las matemáticas y la música que le permitió relacionar las notas musicales con los números racionales. Para realizar sus investigaciones musicales inventó el monocordio, que era un instrumento de una sola cuerda con una caja de resonancia, una regla graduada y un puente variable, que permitía hacer sonar diferentes longitudes de cuerda.
La primera conclusión a la que llegó fue que la frecuencia o altura de un sonido es inversamente proporcional a la longitud de la cuerda: cuanto más larga es la cuerda, más lenta es su vibración y, por tanto, el sonido que produce es más grave y viceversa. Recuerda que el oído humano percibe los sonidos musicales de acuerdo con la frecuencia de la vibración que los produce: percibe como agudos los sonidos con una frecuencia mayor y graves aquéllos con una frecuencia más baja. A partir de ahí estudió las relaciones numéricas entre diferentes longitudes de cuerda que emitían sonidos consonantes, es decir, estudió la sonoridad de los diferentes intervalos.
Aunque los conceptos de consonancia y disonancia han variado a lo largo de la historia y dependen, además, de cuestiones culturales, lo cierto es que Pitágoras constató que los sonidos que se podían expresar como cociente de dos números enteros pequeños (1/2, 3/2, 4/3) resultaban más consonantes que aquellos que respondían a cocientes “raros” (113/47 o 79/34).
.
Pitágoras descubrió que al multiplicar o dividir por dos la frecuencia de una nota cualquiera obtenía justo la misma nota más aguda o más grave. Llegó así a uno de los rasgos fundamentales del oído humano: la relación de octava. El oído percibe como pertenecientes a una misma clase los sonidos que se obtienen al multiplicar o dividir una frecuencia por 2. Este hecho explica que no exista un solo Do (o cualquier otra nota), sino varios, cada uno de ellos en una octava distinta. Cada Do tiene una frecuencia que es el doble de la del Do situado una octava por debajo, y la mitad del situado una octava por encima. Y lo mismo con las notas musicales restantes.
.
LAS ESCALAS
P
ara realizar sus composiciones, los músicos parten de un conjunto de notas que llamamos escala, similar a la paleta de colores de un pintor. Una escala es la división de una octava en distintos sonidos, que se disponen ordenados ascendente o descendentemente. La elección de la escala va a determinar toda la sonoridad de la composición como la elección por el pintor de su paleta de colores va a determinar la tonalidad de sus cuadros. Con una paleta de colores fríos se pueden pintar muchos cuadros diferentes, pero todos van a tener algo en común: una tonalidad fría. De la misma manera, con una escala se pueden componer muchas obras musicales diferentes, pero todas tendrán en común la sonoridad de esa escala. La sonoridad de una escala depende de dos factores: el número de sonidos que la componen y el patrón de distancias (tonos y semitonos) que hay entre ellos. Veamos el ejemplo más importante:
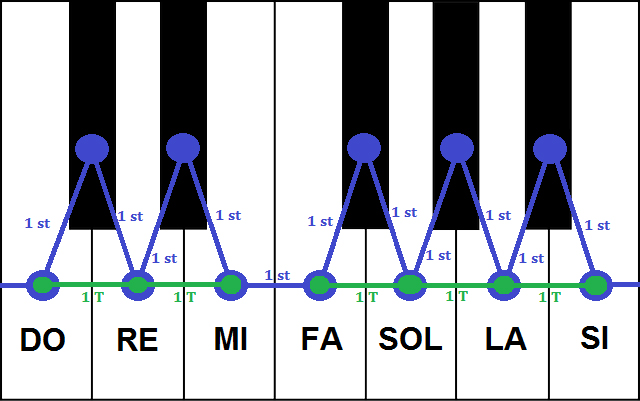
El sistema musical occidental está basado (en su mayor parte) en la denominada escala diatónica, que divide la octava en intervalos de tono y de semitono distribuidos de una forma particular. Los sonidos Do, Re, Mi, Fa, Sol, La y Si constituyen una escala diatónica. La distancia entre dos sonidos adyacentes de esta escala es de un tono, salvo en el caso de los intervalos Mi-Fa y Si-Do (octava), que es de semitono. Por tanto, el esquema de esta escala sería: Tono – Tono – Semitono – Tono – Tono – Tono – Semitono. Muy bien, eso ya lo estudiamos el curso pasado, pero ¿por qué es así?
.
.
.
Antes de seguir adelante, visiona el vídeo sobre las escalas de Jaime Altozano para repasar algunos conceptos…
.
Qué es una escala musical. Jaime Altozano
.
¿Ya? ¡Sigamos adelante!
Volvamos a Pitágoras… Una vez aceptado como punto de partida que para componer una obra musical hay elegir unas notas (una escala), que una frecuencia y su doble suenan bien cuando se tocan simultáneamente y que, además, nuestro oído las reconoce como la misma nota, el problema se reduce a elegir qué otras frecuencias intermedias utilizar entre dos sonidos iguales. Si nuestra nota más grave tiene frecuencia 1 (que llamaremos Do) y, por lo tanto, la de su doble tiene frecuencia 2 (será Do una octava más aguda), ¿qué sonidos intermedios resultan consonantes con la nota fundamental?
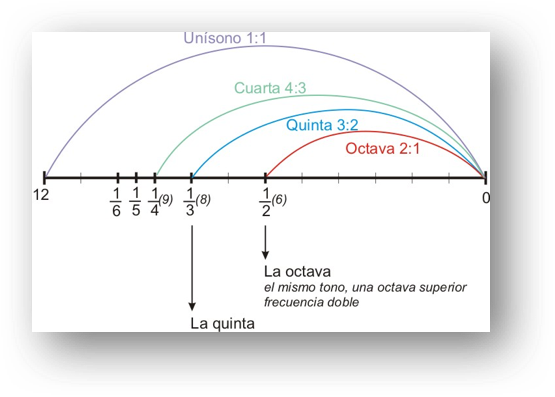
Los pitagóricos se percataron de que los sonidos más consonantes eran aquellos que respondían a cocientes creados con los números 1, 2, 3 y 4:
.
2/1: octava.
3/2: quinta.
4/3: cuarta.
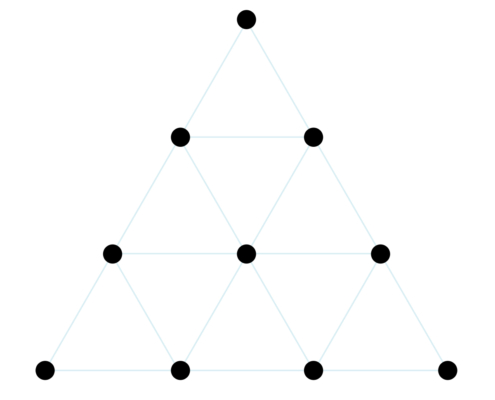
Tan grande les pareció este descubrimiento que a los números 1, 2, 3, 4 les llamaron la Tetraktys y su representación geométrica era la figura sagrada de los pitagóricos dentro de su numerología. En ella estaba encerrado el número perfecto 10 = 1 + 2 + 3 + 4 y en esos cuatro primeros números enteros estaba encerrada ¡toda la armonía musical!
.
Partiendo de la fundamental (por ejemplo, DO), fueron multiplicando las frecuencias por 3/2, es decir, obteniendo quintas sucesivas, hasta llegar de nuevo al DO y cerrar el círculo: DO – SOL – RE – LA – MI – SI – FA – DO´. Cuando la frecuencia obtenida excedía a la del DO agudo la dividían por dos para incluirla dentro de la octava. El resultado de esta operación fue la división de la octava en siete intervalos, cinco de mayor tamaño, que nosotros llamamos tonos, y dos claramente más pequeños que se encuentran entre el MI y el FA y entre el SI y el DO`, que nosotros llamamos semitonos.
En realidad, actualmente aceptamos que un semitono es la mitad de un tono, pero, en realidad, eso no es exactamente así. Las frecuencias obtenidas por los pitagóricos no respondían exactamente a esa proporción en el caso de los intervalos más pequeños (MI – FA y SI –DO) y, por tanto, el círculo de quintas no se cierra de manera matemáticamente exacta. La afinación pitagórica fue efectiva mientras los intervalos armónicos de uso común fueron la octava, la quinta y la cuarta, es decir, durante la Edad Media. Pero a medida que fue desarrollándose la polifonía a partir del siglo XII y durante el Renacimiento esta pequeña diferencia o coma pitagórica mostraba cada vez más su disonancia por lo que se tuvieron que hacer algunos ajustes que dieron lugar a otros sistemas de afinación.
.
La afinación pitagórica. ¡Toda la música está desafinada!
.
Ahora ya conoces el origen y la sonoridad de la escala en la que se basa una gran parte de nuestra música. Sin embargo, la escala diatónica constituye únicamente el material a partir del cual se construye la música. El siguiente paso será organizar o jerarquizar ese material, pero eso lo dejaremos para los próximos apartados…
MODALIDAD
Antes de continuar, repasemos los conceptos clave que ya conocemos hasta este momento:
.
1 Componemos a partir de una serie de notas que llamamos escala.
.
2 La escala divide una octava en varios sonidos que están a distintas distancias.
.
3 Los griegos dividieron la octava en siete sonidos diferentes. Simplificando el tema, en esa división hay cinco distancias mayores (de tono) y dos más pequeñas (de semitono).
.
Llegados a este punto, vamos a empezar a organizarnos… A fin de cuentas, una escala es simplemente un conjunto ordenado de alturas en las que, en principio, no hay un sonido más importante que otro. Para empezar a organizar y jerarquizar los sonidos comencemos con algunos conceptos básicos.
.
Tensión melódica
.
Las notas de una melodía transmiten al oyente distintos grados de tensión. Algunos parámetros tan básicos como la intensidad (más suave, más fuerte) pueden dar más tensión a una nota. Por otro lado, la altura (más grave, más agudo) de una nota es en sí misma un factor de tensión, pues en igualdad de condiciones percibimos las notas agudas como más tensas que las graves.
Las similitudes con la lengua hablada aportan otros factores de tensión a las que denominaremos fraseo: Entonamos de forma distinta una frase enunciativa («Hace frío») que una interrogativa (¿Hace frío?), de modo que la primera marca el fin de de una frase (relajación), mientras que la segunda reclama algún tipo de respuesta (tensión). Un final de frase descendente resultará, en general, más conclusivo que uno ascendente.
Por otro lado, en la música a varias voces existe otro factor que aporta un nuevo y decisivo tipo de tensión: la disonancia. En general, podemos definir la disonancia como aquellos sonidos cuyas frecuencias causan una sensación desagradable a nuestro oido cuando suenan al mismo tiempo.
Observa en la siguiente audición como el compositor, Bernard Herrmann, utiliza estos elementos para llevarnos a las emociones que quiere. ¿Dónde crees que está el punto máximo de tensión?
.
.
La música más terrorífica de la historia del cine.
.
Factores como la altura, el fraseo o la disonancia, nos van a ayudar a crear momentos de tensión y de reposo, y eso acabará asignando a los sonidos de una escala diferentes funciones. De entre todas ellas la más importante de ellas será la tónica, la nota que, dentro de una obra o sección de ella, actúa como sonido de referencia para los demás, donde reposaremos y que actuará como sonido «central». Es el sonido al que le asignaremos más peso e importancia dentro de una composición musical.
En el apartado anterior hemos conocido como construir una escala con siete sonidos entre los que teníamos cinco tonos y dos semitonos siguiendo un patrón T-T-ST-T-T-T-ST. Construimos esa escala a partir de la nota DO, que en esa escala sería la tónica o nota central. Si en vez de construir la escala a partir de DO, lo hacemos a partir de las seis notas restantes obtendremos escalas que tienen los mismos tonos y semitonos pero con distintos patrones (básicamente, los semitonos estarán en distintos sitios), es decir, a partir de las teclas blancas del piano podemos construir siete escalas distintas. Además, ¡la nota tónica o central cambiará en cada una de ellas! Esos patrones diferentes darán lugar a los diferentes MODOS. Veamos el siguiente vídeo de Jaime Altozano en el que nos explica este tema:
.
.
De las siete escalas o modos antiguos, la sonoridad de dos de ellas, la de Do (modo jónico, que nosotros llamamos Mayor) y la de La (modo eólico, que nosotros llamamos modo menor), acabaron imponiéndose en la música occidental, lo que no significa que no se sigan utilizando los demás, como podrás descubrir en el siguiente punto…
.
Escucha…
.
.
A modo de conclusión, hablemos de emociones…
.
Ha llegado el momento de conectar lo que estudiamos en la Unidad 1 sobre el acorde y los intervalos (te recomiendo que repases lo que hablamos sobre acordes mayores, menores, disminuidos, etc.) y todo lo que conocemos ya sobre escalas y modos para hablar de lo importante: la emoción. Porque, a fin de cuentas, la música, es emoción y los compositores utilizan todos los elementos que hemos estudiado como medio para llegar a un fin, que no es otro que expresar lo que quieren y llevar al oyente al terreno emocional que les interesa. En este sentido comparto plenamente la opinión de Jaime Altozano sobre este tema. Si algún día te animas a tocar algún instrumento y te apetece componer algo, no lo olvides: si suena bien, tira toda la teoría a la basura. Sonar bien es siempre más importante que la teoría. Lo importante es hacer lo que quieres sabiendo lo que haces y esa es la única razón por la que hay que conocer las reglas: para saber romperlas apropiadamente.
.
¿Qué emociones producen las 7 escalas modales? – Jaime Altozano
.
TONALIDAD
Llegamos al último punto. Continuemos con el repaso donde lo dejamos en el punto anterior, añadiendo nuevos puntos:
.
1 Componemos a partir de una serie de notas que llamamos escala.
.
2 La escala divide una octava en varios sonidos que están a distintas distancias.
.
3 Los griegos dividieron la octava en siete sonidos diferentes. Simplificando el tema, en esa división hay cinco distancias mayores (de tono) y dos más pequeñas (de semitono).
.
4 Dependiendo de la nota por la que empecemos, los semitonos se situarán en posiciones distintas y obtendremos siete escalas diferentes que llamamos modos. Cada modo tiene una sonoridad diferente y nos permite expresar distintas emociones. De los siete modos, dos han prevalecido sobre los demás en la música occidental: los modos Mayor y menor.
.
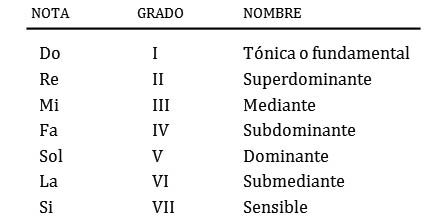
5 Utilizando diferentes recursos para crear tensiones y reposos, jerarquizamos las notas de la escala. La primera nota de cada escala es su tónica, la más importante de todas, la que actuará como «centro de gravedad» al igual que el sol con los planetas de nuestro sistema solar. El resto adquieren diferentes funciones con respecto a la tónica. A cada una de las notas de la escala la llamamos grado. Los grados se ordenan con números romanos y ¡adquieren un nombre que define su función dentro de todo este universo!
Un poco más arriba hablamos de la disonancia como recurso para crear tensión. Para conseguir disonancias tenemos que hacer sonar varios sonidos al mismo tiempo, al menos dos, por tanto tenemos que hablar de acordes. Ha llegado el momento de construir acordes sobre las notas de las escala, crear tensiones y distensiones entre ellos, y unir así todo lo aprendido en la Unidad 1 y 2 sobre organización sonora: bienvenidos a la tonalidad.
ACTIVIDADES INTERACTIVAS
.
NOTA: Algunas letras del rosco de pasapalabra hacen alusión a compositores clásicos que no encontrarás en el tema. ¡Tendrás que buscar la solución en internet! ;-)
AUDICIONES
LECTURA RÍTMICA
DICTADOS
4/4
.
.
.
.
.
.
.
.
.
3/4
.
DICTADO 1
.
DICTADO 2
.
DICTADO 3
.
DICTADO 4
.
DICTADO 5
.
DICTADO 6
.
DICTADO 7
.
DICTADO 8
.