MUSIC AND MATHEMATICS. THE DIATONIC SCALE
.
B
ut… Where did it all begin? Where do we place the origins of Western music? To answer these questions we will have to take a long journey back in time to Ancient Greece and get to know the school that Pythagoras of Samos founded in the mid-sixth century BC.
Pythagoras discovered a connection between mathematics and music that allowed him to relate musical notes to rational numbers. To carry out his musical research he invented the monochord, which was a single-stringed instrument with a sounding board, a graduated ruler and a variable bridge, which allowed different string lengths to be played.
The first conclusion he reached was that the frequency or pitch of a sound is inversely proportional to the length of the string: the longer the string, the slower its vibration and, therefore, the sound it produces is lower and vice versa. Remember that the human ear perceives musical sounds according to the frequency of the vibration that produces them: it perceives as high-pitched sounds those with a higher frequency and low-pitched sounds those with a lower frequency. From there he studied the numerical relations between different lengths of string that emitted consonant sounds, that is, he studied the sonority of the different intervals.
Although the concepts of consonance and dissonance have varied throughout history and also depend on cultural issues, the truth is that Pythagoras noted that the sounds that could be expressed as the quotient of two small whole numbers (1/2, 3/2, 4/3) were more consonant than those that responded to «rare» quotients (113/47 or 79/34).
Pythagoras discovered that by multiplying or dividing by two the frequency of any one note he obtained just the same higher or lower note. He thus arrived at one of the fundamental features of the human ear: the octave ratio. The ear perceives as belonging to the same class the sounds obtained by multiplying or dividing a frequency by 2. This fact explains that there is not only one C (or any other note), but several, each one in a different octave. Each C has a frequency that is twice as high as the C one octave below it, and half as high as the C one octave above it. And the same with the remaining musical notes.
.
SCALES
.
T
o make their compositions, the musicians start from a set of notes that we call scale, similar to the color palette of a painter. A scale is the division of an octave into different sounds, which are arranged in ascending or descending order. The choice of the scale will determine all the sonority of the composition as the choice by the painter of his color palette will determine the tonality of his paintings. With a palette of cold colors you can paint many different pictures, but all will have something in common: a cold tone. In the same way, with a scale you can compose many different musical works, but they will all have in common the sonority of that scale. The sonority of a scale depends on two factors: the number of sounds that compose it and the pattern of distances (tones and semitones) between them. Let’s see the most important example.
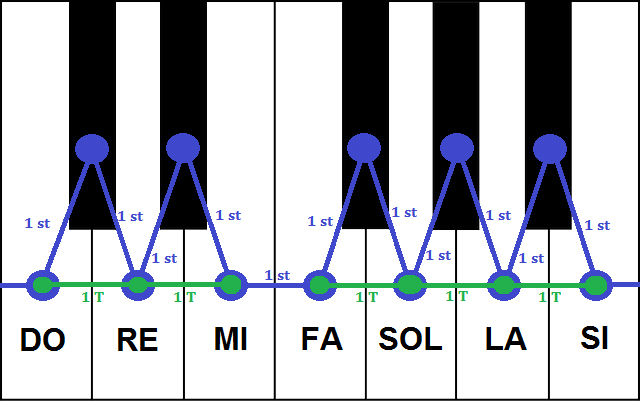
The Western musical system is based (for the most part) on the so-called diatonic scale, which divides the octave into intervals of tones and semitones distributed in a particular way. The sounds C, D, E, F, G, A and B constitute a diatonic scale. The distance between two adjacent sounds of this scale is one tone, except in the case of the intervals E-F and B-C (octave), which is semitone. Therefore, the scheme of this scale would be: Tone – Tone – Semitone – Tone – Tone – Tone – Semitone. Very well, we already studied this last course, but why is it like this?
.
.
.
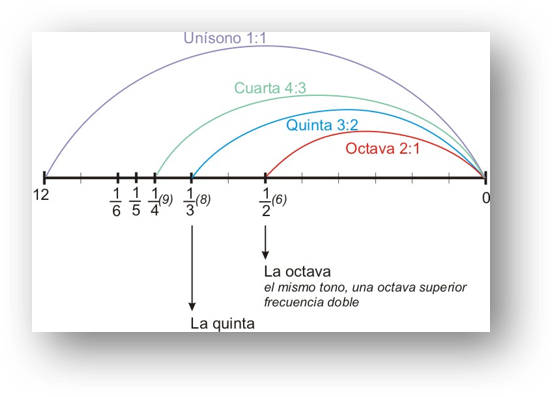
Let’s go back to Pythagoras… Once accepted as a starting point to compose a piece of music you have to choose some notes (a scale), that a frequency and its octave sound blended when played simultaneously and that, in addition, our ear recognizes them as the same note. The problem is reduced to choosing what other intermediate frequencies to use between two equal sounds. If our lowest note has frequency 1 (which we will call C) and, therefore, its double has frequency 2 (it will be C an octave higher), which intermediate sounds are consonant with the fundamental note?
The Pythagoreans realized that the most consonant sounds were those that responded to quotients created with the numbers 1, 2, 3 and 4:
.
2/1: octave.
3/2: fifth.
4/3: fourth.
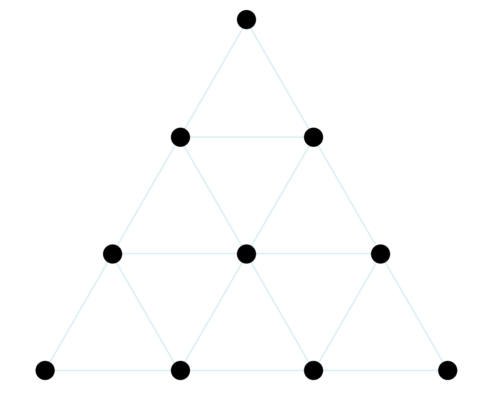
They found this discovery so great that the numbers 1, 2, 3, 4 were called the Tetraktys and their geometric representation was the sacred figure of the Pythagoreans within their numerology. In it was enclosed the perfect number 10 = 1 + 2 + 3 + 4 and in those first four whole numbers was enclosed all the musical harmony!
.
Starting from the fundamental (for example, C), they multiplied the frequencies by 3/2, that is, obtaining successive fifths, until they reached the C again and closed the circle: C – D – F – G – A – B – C´. When the frequency obtained exceeded the acute C they divided it by two to include it within the octave. The result of this operation was the division of the octave into seven intervals, five of which are larger, which we call tones, and two clearly smaller ones which are between the E and the F and between the B and the C, which we call semitones.
Actually, we currently accept that a semitone is half a tone, but, in reality, that is not exactly so. The frequencies obtained by the Pythagoreans did not respond exactly to that proportion in the case of the smaller intervals (E – F and B – C) and, therefore, the circle of fifths does not close in a mathematically exact way. The Pythagorean tuning was effective while the commonly used harmonic intervals were the octave, fifth and fourth, i.e. during the Middle Ages. But as polyphony developed from the 12th century and during the Renaissance, this small difference or Pythagorean coma showed more and more its dissonance, so some adjustments had to be made that gave rise to other tuning systems.
Now you know the origin and the sonority of the scale on which a large part of our music is based. However, the diatonic scale constitutes only the material from which the music is constructed. The next step will be to organize and prioritize that material, but we will leave that for the next sections…
MODALITY
.
Before we continue, let’s review the key concepts we already know up to this point:
.
1 We compose from a series of notes that we call scale.
.
2 The scale divides an octave into several sounds that are at different distances.
.
3 The Greeks divided the octave into seven different sounds. Simplifying the matter, in that division there are five major distances (TONES) and two smaller ones (SEMITONES).
.
At this point, let’s start organizing… In the end, a scale is simply an ordered set of pitches where, in principle, there is no one sound more important than another. To start organizing and prioritizing the sounds let’s start with some basic concepts.
.
Melodic tension
.
The notes of a melody transmit different degrees of tension to the listener. Some basic parameters such as intensity (softer, stronger) can give more tension to a note. On the other hand, the pitch (lower, higher) of a note is in itself a factor of tension, since all other things being equal, we perceive high notes as more tense than low ones.
The similarities with the spoken language bring other tension factors to what we will call phrasing: We intone an enunciative phrase («It’s cold») differently than an interrogative one (Is it cold?), so that the first one marks the end of a phrase (relaxation), while the second one calls for some kind of response (tension). A descending end of the sentence will be, in general, more conclusive than an ascending one.
On the other hand, in multi-voice music there is another factor that brings a new and decisive type of tension: dissonance. In general, we can define dissonance as those sounds whose frequencies cause an unpleasant sensation to our ear when they sound at the same time.
Observe in the following audition how the composer, Bernard Herrmann, uses these elements to lead us to the emotions he wants. Where do you think the maximum point of tension is?
.
.
Factors such as pitch, phrasing or dissonance will help us to create moments of tension and rest, and this will end up assigning different functions to the sounds of a scale. Of all of them the most important will be the tonic, the note that, within a work or section of it, acts as a reference sound for the others, where we will rest and that will act as a «central» sound. It is the sound to which we will assign more weight and importance within a musical composition.
In the previous section we have known how to build a scale with seven sounds among which we had five tones and two semitones following a T-T-ST-T-T-ST pattern. We build that scale from the note C, that in that scale would be the tonic or central note. If instead of building the scale from C, we do it from the six remaining notes we will get scales that have the same tones and semitones but with different patterns (basically, the semitones will be in different places), that is, from the white keys of the piano we can build seven different scales. In addition, the tonic or center note will change in each of them! These different patterns will give rise to the different MODES.
.
Of the seven ancient scales or modes, the sonority of two of them, C (Ionian, which we call Major) and A (Aeolian, which we call Minor), ended up imposing themselves on Western music, which does not mean that the others are no longer used, as you will discover in the following section…
.
TONALITY
.
We reached the last point. Let’s continue with the review where we left off in the previous point, adding new points:
.
1 We compose from a series of notes that we call scale.
.
2 The scale divides an octave into several sounds that are at different distances.
.
3 The Greeks divided the octave into seven different sounds. Simplifying the matter, in that division there are five major distances (TONES) and two smaller ones (SEMITONES).
.
4 Of the seven ancient scales or modes, the sonority of two of them, C (Ionic mode, which we call Major) and A (Aeolian mode, which we call Minor), ended up imposing themselves on Western music, which does not mean that the others are no longer used, as you will discover in the following point… Each mode has a different sonority and allows us to express different emotions. Of the seven modes, two have prevailed over the others in Western music: the Major and Minor modes.
.
5 By using different resources to create tension and rest, we prioritize the notes of the scale. The first note of each scale is its tonic, the most important of all, which will act as the «center of gravity» just as the sun does with the planets of our solar system. The rest acquire different functions with respect to the tonic. We call each one of the notes of the scale degree. The degrees are ordered with Roman numerals and acquire a name that defines their function within this entire universe!
A little further up we talked about dissonance as a resource for creating tension. To achieve dissonance we have to play several sounds sound at the same time, at least two, so we have to talk about chords. Now it´s the moment to build chords on the notes of the scales, to create tension and distension between them, and thus unite everything learned in Unit 1 and 2 about sound organization: welcome to the tonality.